比较器offset论文研读

笔者最近在做比较器的相关电路，需要仿真offset，如果 VFS=1VV_{FS}=1V ，并且是10Bits的ADC的话，则要求offset满足 VOS<12LSB=0.48mVV_{OS}<\frac{1}{2}LSB=0.48mV 。因此仿真计算比较器的offset有重大意义。

遗憾的是笔者在某宝买的虚拟机没有mis模型，跑不了蒙卡，因此笔者也就萌生出了手算offset的想法，故也就有了本文。

offset定义

offset定义：当比较器输出达到 VDD2\frac{V_{DD}}{2} 时，输入端 VinV_{in} 和 VipV_{ip} 的差值。

首先offset由系统失配和随机失配带来。系统失配指的是电路本身设计所带来的，如下图所示：

系统失配

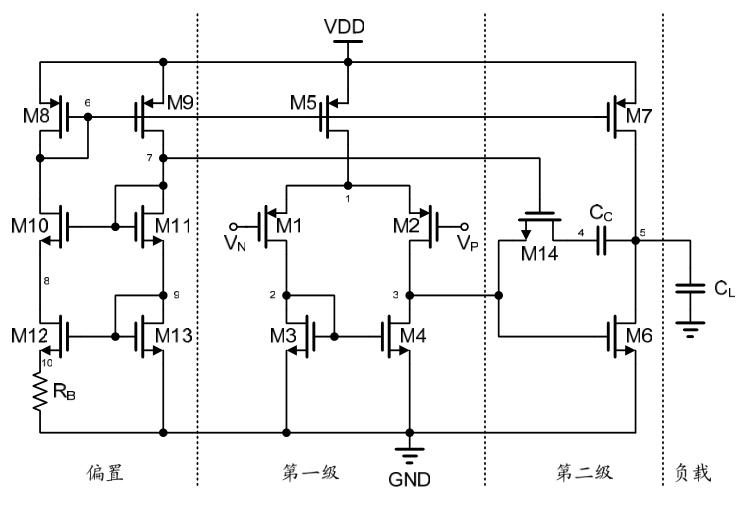
图1 二级运放电路图

在图1的二级运放电路图中我们需要保证M3、M4、M6的 VGSV_{GS} 一致，即若实际直流工作点存在偏差的话则会贡献有一部分offset，本文重点分析random mismatch带来的offset。

随机失配

在实际芯片生产过程中，存在梯度效应，简单来说就是工艺生产的不均匀性，所以可能存在沿某一方向某一指标的持续恶化，例如沿东南方向电子迁移率持续降低。这和Layout时尽量对角对称的初衷差不多。本文重点分析关于导通电压 VTHV_{TH} 和迁移率 μ\mu 的mismatch，结合文中的结论，它近似满足如下分布：

σTH2=AVt2W⋅L+SVT2⋅D2σμi/μn2=Aμ2W⋅L+Sμ2⋅D2\begin{aligned} \sigma_{TH}^{2} &= \frac{A_{Vt}^{2}}{W\cdot L}+ S_{V_{T}}^{2} \cdot D^{2} \\ \sigma_{\mu_{i}/\mu_{n}}^{2} &= \frac{A_{\mu}^{2}}{W\cdot L}+ S_{\mu}^{2} \cdot D^{2} \end{aligned}

其中 AVtA_{Vt} 为制造工艺决定的常数，DD 为chip中各pair管子之间的距离。

其中的具体参数可以参考下方链接中的文档，也可参考下方的图2图3所示：

https://bbs.eetop.cn/thread-988998-1-1.html

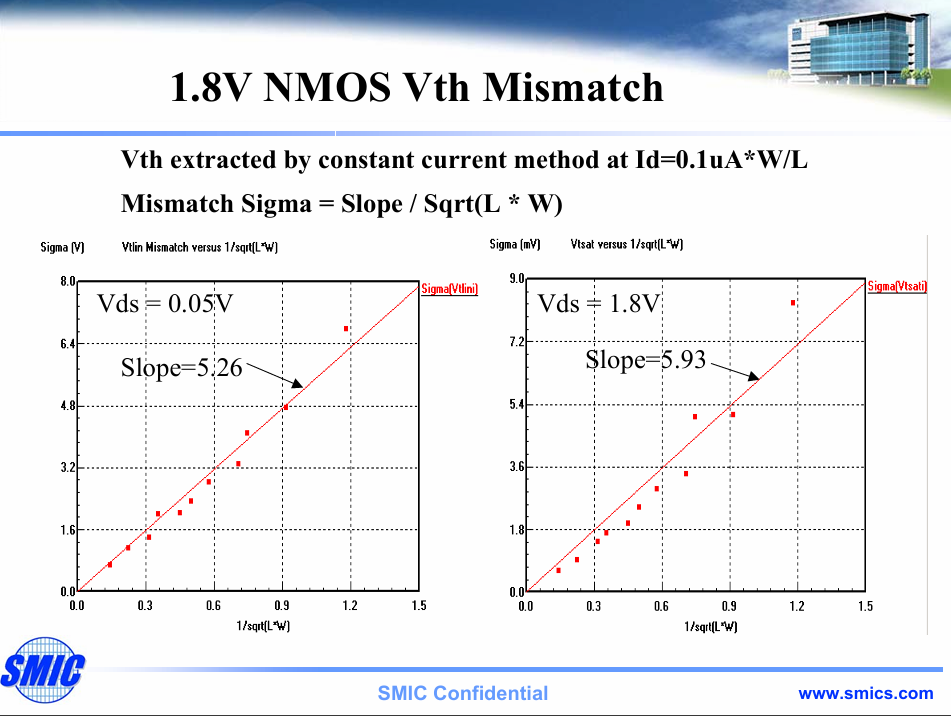
图2 n18 mismatch

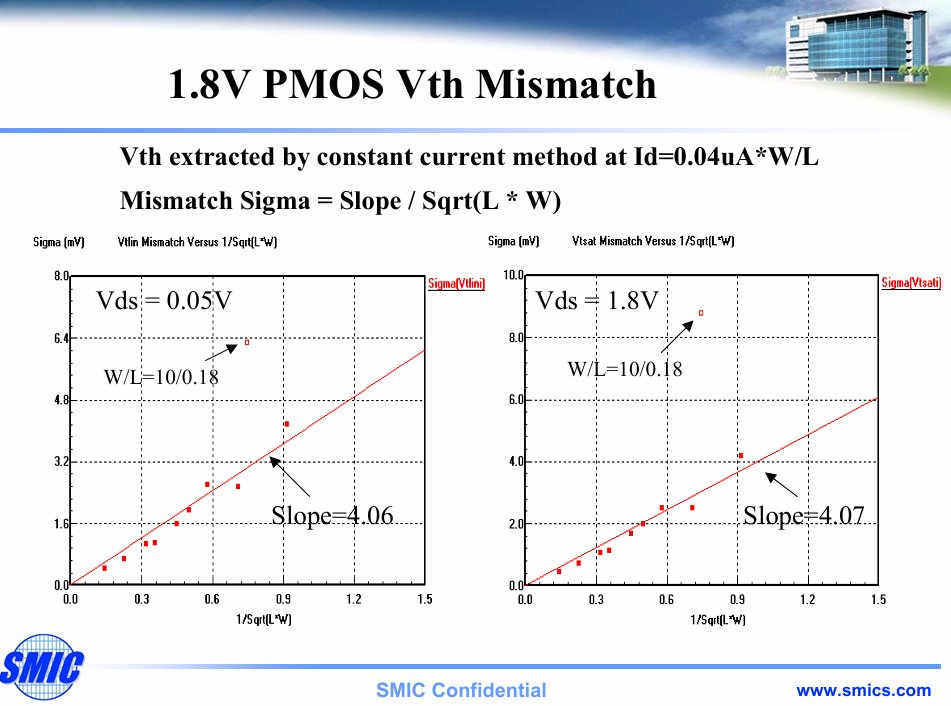
图3 p18 mismatch

手算offset

OK回归主题，开始计算offset。本文以图4所示的Lewis-Gray型动态比较器结构来分析：

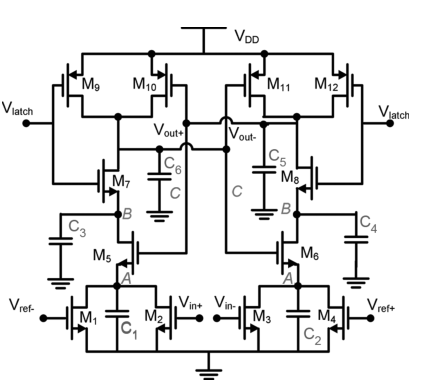
图4 比较器结构图

思路十分简单：从KCL出发，将M5-M6 pair，M7-M8 pair，M10-M11 pair的电流与M1-M2、M3-M4的电流关联起来，同时通过KCL做差求解 VOS=Vin+−Vin−V_{OS} = V_{in+} - V_{in-} 。

思路就是这样，下面是具体的分析过程，为了考虑 VTHV_{TH} 和迁移率 μ\mu 的mismatch，我们考虑如下形式引入微小变化量，以M5-M6 pair为例：

μ5=μn+Δμ5μ6=μn+Δμ6Vt5=Vtn+ΔVt5Vt6=Vtn+ΔVt6\begin{aligned} \mu_{5} &= \mu_{n} + \Delta \mu_{5} \\ \mu_{6} &= \mu_{n} + \Delta \mu_{6} \\ V_{t5} &= V_{tn} + \Delta V_{t5} \\ V_{t6} &= V_{tn} + \Delta V_{t6} \end{aligned}

考虑如下KCL方程：

ID5=ID1+ID2ID6=ID3+ID4\begin{aligned} I_{D5} &= I_{D1} + I_{D2} \\ I_{D6} &= I_{D3} + I_{D4} \end{aligned}

进而通过求解 Vin+−Vin−V_{in+} - V_{in-} 求解 VOSV_{OS}。

阈值电压和迁移率mismatch的计算结果

本文基于如下简化分析，讨论：

选择 VlatchV_{latch} 刚达到 VDDV_{DD} 时的时刻来分析；所有管子具有相同的栅长 LL ；M1-M4具有相同的尺寸；同时各管子工作在如下工作区：

管子 工作区
M1-M4 三极管区
M5-M6 饱和区
M7-M8 三极管区
M10-M11 饱和区

其中M9和M12的mismatch影响可以忽略不记。同时考虑 VTHV_{TH} 和 μ\mu 的失配服从Guassian分布，则各pair管子所贡献的 VOSV_{OS} 的方差满足下列式子：

σVOS−M5M62=(Vout+−Vs5−VtnVs5⋅W5W1)2⋅σVt52+(Vout−−Vs6−VtnVs6⋅W6W1)2⋅σVt62+((Vout+−Vs5−Vtn)22⋅Vs5⋅W5W1)2⋅σμ5/μn2+((Vout−−Vs6−Vtn)22⋅Vs6⋅W6W1)2⋅σμ6/μn2\begin{aligned} \sigma_{V_{OS}-M5M6}^{2} &= (\frac{V_{out+}-V_{s5}-V_{tn}}{V_{s5}}\cdot \frac{W_{5}}{W_{1}})^{2} \cdot \sigma_{V_{t5}}^{2} + (\frac{V_{out-}-V_{s6}-V_{tn}}{V_{s6}}\cdot \frac{W_{6}}{W_{1}})^{2} \cdot \sigma_{V_{t6}}^{2} \\ &+(\frac{(V_{out+}-V_{s5}-V_{tn})^{2}}{2\cdot V_{s5}}\cdot \frac{W_{5}}{W_{1}})^{2} \cdot \sigma_{\mu_{5}/\mu_{n}}^{2} + (\frac{(V_{out-}-V_{s6}-V_{tn})^{2}}{2\cdot V_{s6}}\cdot \frac{W_{6}}{W_{1}})^{2} \cdot \sigma_{\mu_{6}/\mu_{n}}^{2} \end{aligned}

σVOS−M1M42=σVt12+σVt42+(Vref−−Vtn)2⋅σμ1/μn2+(Vref+−Vtn)2⋅σμ4/μn2\begin{aligned} \sigma_{V_{OS}-M1M4}^{2} &= \sigma_{V_{t1}}^{2} + \sigma_{V_{t4}}^{2} +(V_{ref-}-V_{tn})^{2} \cdot \sigma_{\mu_{1}/\mu_{n}}^{2} + (V_{ref+}-V_{tn})^{2} \cdot \sigma_{\mu_{4}/\mu_{n}}^{2} \end{aligned}

σVOS−M2M32=σVt22+σVt32+(Vin+−Vtn)2⋅σμ2/μn2+(Vin−−Vtn)2⋅σμ3/μn2\begin{aligned} \sigma_{V_{OS}-M2M3}^{2} &= \sigma_{V_{t2}}^{2} + \sigma_{V_{t3}}^{2} +(V_{in+}-V_{tn})^{2} \cdot \sigma_{\mu_{2}/\mu_{n}}^{2} + (V_{in-}-V_{tn})^{2} \cdot \sigma_{\mu_{3}/\mu_{n}}^{2} \end{aligned}

σVOS−M10M112=(VDD−Vout+−Vtp3⋅Vs5)2⋅σVt102+(VDD−Vout+−Vtp3⋅Vs6)2⋅σVt112+((VDD−Vout+−Vtp)26⋅Vs5)2⋅σμ5/μn2+((VDD−Vout+−Vtp)26⋅Vs6)2⋅σμ6/μn2\begin{aligned} \sigma_{V_{OS}-M10M11}^{2} &= (\frac{V_{DD}-V_{out+}-V_{tp}}{3\cdot V_{s5}})^{2} \cdot \sigma_{V_{t10}}^{2} + (\frac{V_{DD}-V_{out+}-V_{tp}}{3\cdot V_{s6}})^{2} \cdot \sigma_{V_{t11}}^{2} \\ &+(\frac{(V_{DD}-V_{out+}-V_{tp})^{2}}{6\cdot V_{s5}})^{2} \cdot \sigma_{\mu_{5}/\mu_{n}}^{2} + (\frac{(V_{DD}-V_{out+}-V_{tp})^{2}}{6\cdot V_{s6}})^{2} \cdot \sigma_{\mu_{6}/\mu_{n}}^{2} \end{aligned}

σVOS−M7M82=(W7W2⋅Vds7Vs5)2⋅σVt72+(W7W2⋅Vds7Vs5)2⋅(Vlatch−Vd5−Vtn−Vds72)2⋅σμ7/μn2+(W8W2⋅Vds8Vs5)2⋅σVt82+(W8W2⋅Vds8Vs5)2⋅(Vlatch−Vd5−Vtn−Vds82)2⋅σμ8/μn2\begin{aligned} \sigma_{V_{OS}-M7M8}^{2} &= (\frac{W_{7}}{W_{2}} \cdot \frac{V_{ds7}}{V_{s5}} )^{2} \cdot \sigma_{V_{t7}}^{2} + (\frac{W_{7}}{W_{2}} \cdot \frac{V_{ds7}}{V_{s5}} )^{2}\cdot ( V_{latch}-V_{d5}-V_{tn}-\frac{V_{ds7}}{2} )^{2} \cdot \sigma_{\mu_{7}/\mu_{n}}^{2} \\ &+ (\frac{W_{8}}{W_{2}} \cdot \frac{V_{ds8}}{V_{s5}} )^{2} \cdot \sigma_{V_{t8}}^{2} + (\frac{W_{8}}{W_{2}} \cdot \frac{V_{ds8}}{V_{s5}} )^{2}\cdot ( V_{latch}-V_{d5}-V_{tn}-\frac{V_{ds8}}{2} )^{2} \cdot \sigma_{\mu_{8}/\mu_{n}}^{2} \end{aligned}

考虑到每对pair的管子的mismatch是独立分布的，因此总的 VOSV_{OS} 满足下式：

σVOS=(σVOS−M5M62+σVOS−M1M42+σVOS−M2M32+σVOS−M7M82+σVOS−M10M112)1/2\begin{aligned} \sigma_{V_{OS}} =( \sigma_{V_{OS}-M5M6}^{2} + \sigma_{V_{OS}-M1M4}^{2} + \sigma_{V_{OS}-M2M3}^{2} + \sigma_{V_{OS}-M7M8}^{2} +\sigma_{V_{OS}-M10M11}^{2} )^{1/2} \end{aligned}

下面这张图是40nm下比较器的offset的蒙卡仿真结果与手算结果的比较：

图5 40nm下比较器的offset的蒙卡仿真结果与手算结果的比较

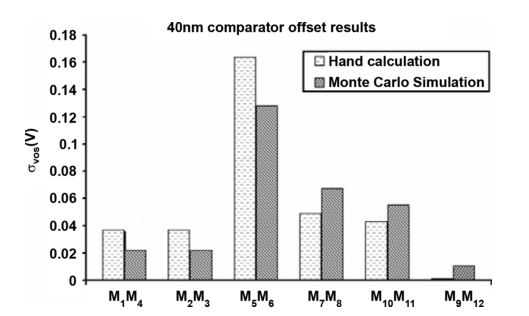
总体符合拉扎维先生在**《The Design of a Comparator》**一文中提出的结论:在一个典型的设计中，当把M7和M8之间的失调等效到输入端时，需要先除以一个大约为 Av=10A_{v}=10 的因子（第二阶段的增益倍率）；而当M10、M11导致的失调等效到输入端时，需要除以一个大约为10的因子，这是因为考虑到了M10、M11管只有在最后两个阶段的时候才导通。

但是拉扎维先生论文中比较器的电路和本文讨论的略有不同。

寄生电容mismatch的计算结果

此处先给出一些典型值，1fF的电容失配可能会带来输出结点几十毫伏的输入参考失配电压。其中包含寄生电容的比较器结构图如下图所示：

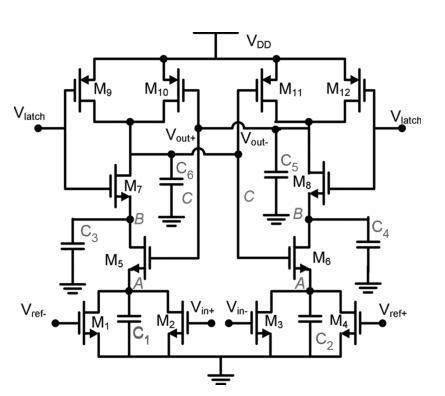
图6 比较器内部寄生电容图示

为简化分析，只讨论输出节点的寄生电容 C5C_{5} 和 C6C_{6} ，同时忽略其他电容的分流作用，因此得到如下方程:

C5dVout−dt=Ids1+Ids2C6dVout+dt=Ids3+Ids4dVout−dt=dVout+dt\begin{aligned} C_{5} \frac{dV_{out-}}{dt} =& I_{ds1} + I_{ds2}\\ C_{6} \frac{dV_{out+}}{dt} =& I_{ds3} + I_{ds4}\\ \frac{dV_{out-}}{dt} &=\frac{dV_{out+}}{dt} \end{aligned}

同时考虑 C5C_{5} 和 C6C_{6} 之间存在微小失配，即有下式：

C5=C6+ΔC56\begin{aligned} C_{5} = C_{6} + \Delta C_{56} \end{aligned}

进而得到:

VOS,C56=ΔC56C6Ids3+Ids4μnCoxW2L2Vds1\begin{aligned} V_{OS,C56} = \frac{\Delta C_{56}}{C_{6}} \frac{I_{ds3}+I_{ds4}}{\mu_{n}C_{ox}\frac{W_{2}}{L_{2}}V_{ds1}} \end{aligned}

总结

调整为下图所示的拓扑结构可以优化offset表现:

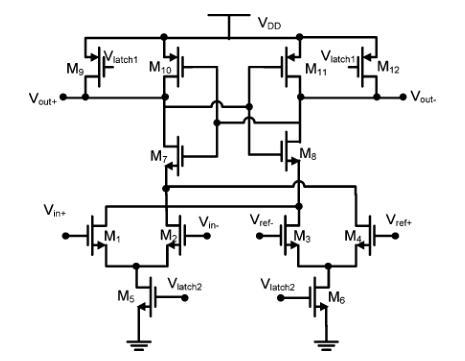
图7 比较器结构图2

不愧是TCAS-I的文章，读起来就是通畅。

参考文献：

  1. Analyses of Static and Dynamic Random Offset Voltages in Dynamic Comparators
  1. https://wx.seu.edu.cn/_upload/article/files/78/6c/091d364c47e288410db0cc79f7a8/3ba08ec5-4c20-43fa-b82d-a7d9aff7ccd3.pdf